Golombovo kódování

Golombovo kódování je bezeztrátová kompresní metoda patřící do skupiny kódu vynalezených Solomonem W. Golombem v 60. letech. Pro takové abecedy, které mají geometrické rozdělení pravděpodobnosti, bude Golombovo kódování optimální a bude tvořit prefixový kód. Z této vlastnosti plyne, že toto kódování bude velmi vhodné pro takové případy, kdy pravděpodobnost malých hodnot na vstupu bude mnohonásobně vyšší než pravděpodobnost velkých.

Ricovo kódování (podle Roberta F. Ricea) označuje podmnožinu Golombových kódů, které vytvářejí jednodušší (ale teoreticky suboptimální) prefixový kód. Rice použil tuto množinu kódů v rámci adaptivního kódování; "Riceovo kódování" tak může odkazovat buď na toto adaptivní kódování, nebo na speciální podmnožinu Golombových kódů. Zatímco v obecném Golombově kódování může být volitelný parametr $M$ libovolné kladné celé číslo, Riceovo kódování volí parametr tak, aby byl mocninou dvou. Tato vlastnost činí Riceovo kódování vhodnějším pro počítačové využití, protože násobení a dělení dvěma je v binární aritmetice mnohem efektivnější.

Riceovo kódování se používá v mnoha bezeztrátových kompresních algoritmech pro obrázky a zvuk.

Přehled

Tvorba kódu

Golombovo kódování používá nastavitelný parametr M k tomu, aby vstupní hodnoty rozdělilo na dvě části: $q$, výsledek celočíselného dělení M a $r$ zbytek po dělení. Hodnota $q$ se zakóduje pomocí unárního kódování a je následována zbytkem zakódovaným pomocí zkráceného binárního kódování. Pokud $M=1$, pak je Golombovo kódování shodné s unárním.

Golomb-Riceovo kódování si můžeme představit jako zakódování čísla pomocí pozice q a posunu r. Obrázek výše ukazuje pozici q a posun r pro kódování čísla N za použití Golomb-Riceova kódování s parametrem M.

Formálně jsou dvě části definovány následujícím výrazem, kde $x$ je číslo, které chceme zakódovat: $q=\lfloor \frac{\left(x-<!--\; -\; -->1\right)}{M}\rfloor$ a $r=x-<!--\; -\; -->qM-<!--\; -\; -->1$ Konečný výsledek pak je: $\left(q+1\right)r$.

$r$ se může sestávat z proměnlivého počtu bitů, speciálně z b bitů pro Riceovo kódování, v případě Golombova kódování se mění mezi b-1 a b bity. Nechť $b=\lceil <!--\; \lceil \; -->{\log }_2<!--\; \; -->\left(M\right)\rceil <!--\; \rceil \; -->$. Když , pak se použije b-1 bitů pro zakódování r, pokud pak se použije b bitů. Je zřejmé, že $b={\log }_2<!--\; \; -->\left(M\right)$ pokud M je mocnina dvou tak můžeme zakovat všechny hodnoty r pomocí b bitů.

Parametr M je funkcí odpovídajícího Bernouliho procesu, který je parametrizován pomocí $p=P(X=0)$ pravděpodobností úspěchu daného binomického rozdělení. $M$ je buď mediánem daného rozdělení, nebo medián +/- 1. Můžeme ho odvodit z následujících nerovností:

Golomb ve své práci tvrdí, že pro velká M je velmi malý postih, když vybereme $M=\lfloor \frac{-<!--\; -\; -->1}{{\log }_2<!--\; \; -->(1-<!--\; -\; -->p)}\rfloor$.

Golombovo kování je ekvivalentní Huffmanovu kódování pro zadané pravděpodobnosti, kdyby bylo možné vytvořit Huffmanův kód (což pro geometrické rozdělení nejde, neboť se nejedná o diskrétní rozdělení).

Případ s celými čísly

Golombovo bylo navrženo k zakódování sekvencí nezáporných čísel. Může být ale snadno rozšířeno tak, aby bylo schopné zakódovat i obecné posloupnosti celých čísel. Všem vstupním hodnotám přiřadíme nové hodnoty z množiny celých kladných čísel, tak aby byly unikátní a mohli jsme je později přiřadit zpět. Posloupnost začínající: 0,-1,1,-2,2,-3,3,-4,5 … n-tá negativní hodnota (tj. -n) je namapována jako n-té liché číslo (2n-1), a m-té kladné číslo je vyjádřeno jako m-té sudé číslo (2m). Optimální prefixový kód vznikne jen v případě, že kladná čísla a hodnoty záporných čísel odpovídají tomu samému geometrickému rozdělení.

Jednoduchý algoritmus

Následující algoritmus popisuje, jak zakódovat hodnotu na vstupu pomocí Rice-Golombova kódování.

1. Zaokrouhlit M na celočíselnou hodnotu.
2. Pro číslo N, které chceme zakódovat, najděme
   1. podíl = q = int[N/M]
   2. zbytek = r = N mod M
3. Vygenerujeme kódové slovo
   1. Formát kódu : <zakódovaný podíl><zakódovaný zbytek>, kde
   2. zakódovaný podíl je (zakódován unárně)
      1. Zakódujeme q jako sekvenci q 1 a na konec přidáme 0
   3. kód zbytku je (zakódován zkráceně binárně)
      1. Když M je mocnina dvou, bude potřeba ${\log }_2<!--\; \; -->\left(M\right)$ bitů. (Riceovo kódování)
      2. Když M není mocnina 2, tak $b=\lceil <!--\; \lceil \; -->{\log }_2<!--\; \; -->\left(M\right)\rceil <!--\; \rceil \; -->$
         1. Když zakódujeme r pomocí standardního binárního kódování délky b-1 bitů.
         2. Když $r\ge <!--\; \ge \; -->2^b-<!--\; -\; -->M$ zakódujeme číslo $r+2^b-<!--\; -\; -->M$ pomocí standardního binárního kódování o délce b bitů.

Příklad

Nastavme M = 10. Tedy $b=\lceil <!--\; \lceil \; -->{\log }_2<!--\; \; -->\left(10\right)\rceil <!--\; \rceil \; -->=4$. Ořez pak bude $2^b-<!--\; -\; -->M=16-<!--\; -\; -->10=6$

Například pro Golomb-Rice kódování s parametrem M=10 a číslem pro zakódování 42 se nejprve spočítá q=4 a r=2. Pak se obě částí zakódují q=11110 a r=010 a výsledné kódové slovo vznikne složením těchto dvou částí. Části už není potřeba od sebe oddělovat, protože první část poznáme snadno – končí tam, kde se poprvé objeví nula.

Ukázkový kód algoritmu

Tento základní kód předpokládá Riceovo kódování, tedy že M=2^k.

Zakódování

 void golombEncode(char* vstup, char* vystup, int M)
 {
     IntReader intreader(vstup);
     BitWriter bitwriter(vystup);
     while(intreader.hasLeft())
     {
         int num = intreader.getInt();
         int q = num / M;
         for (int i = 0 ; i < q; i++)
             bitwriter.putBit(true);   // zapíše q jedniček
         bitwriter.putBit(false);      // zapíše jednu nulu
         int v = 1;
         for (int i = 0 ; i < log2(M); i++)
         {            
             bitwriter.putBit( v & num );  
             v = v << 1;         
         }
     }
     bitwriter.close();
     intreader.close();
 }

Dekódování

 void golombDecode(char* vstup, char* vystup, int M)
 {
     BitReader bitreader(vstup);
     IntWriter intwriter(vystup);
     int q = 0;
     int nr = 0;
     while (bitreader.hasLeft())
     {
         nr = 0;
         q = 0;
         while (bitreader.getBit()) q++;     
         for (int a = 0; a < log2(M); a++)   
             if (bitreader.getBit())
                 nr += 1 << a;
         nr += q*M;                          
         intwriter.putInt(nr);               
     }
     bitreader.close();
     intwriter.close();
 }

Použití pro run-length kódování

Máme-li abecedu o dvou symbolech, nebo množinu dvou událostí P a Q s pravděpodobnostmi p a (1 – p), kde $p\ge <!--\; \ge \; -->\frac{1}{2}$. Golombovo kódování může být použito k zakódování nula nebo více P oddělených jedním Q. V takovém případě je nejlepší nastavit parametr M jako nejbližší celé číslo k $\frac{-<!--\; -\; -->1}{{\log }_2<!--\; \; -->p}$. Když $p=\frac{1}{2}$, M = 1 a Golombovo kódování je shodné s unárním.

Aplikace

Riceovo kódování je použito v několika kódech pro zpracování signálu pro predikci zbytků. V prediktivních algoritmech, kde zbytky mají tendenci se rozdělit tak, že odpovídají dvoustrannému geometrickému rozdělení s malými zbytky častějšími než velkými, Riceův kód téměř odpovídá Huffmanovu kódu pro dané rozdělení s tou výhodou, že nemusí přenášet Huffmanovu tabulku. Jediný signál, který neodpovídá geometrickému rozdělení je sinová vlna, kde jsou velké a malé zbytky podobně pravděpodobné.

Několik bezeztrátových zvukových kompresních algoritmů jako jsou Shorten,^[1] FLAC,^[2] Apple Lossless, a MPEG-4 ALS používá Riceovo kódování v rámci svého kódovacího procesu. Riceovo kódování je také použito pro bezeztrátovou kompresi obrázků FELIICS.

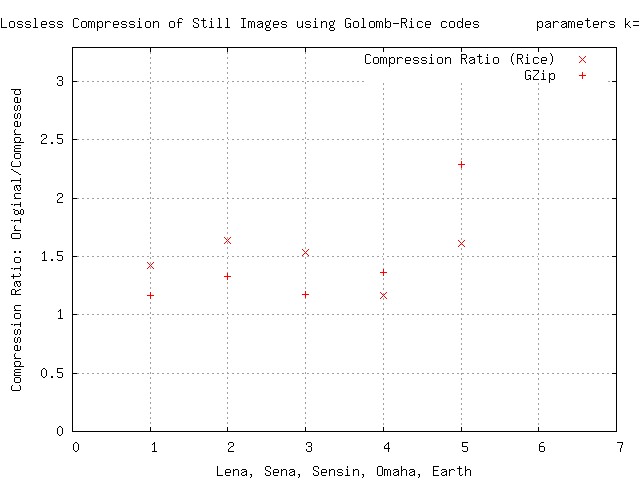
Rice-Golombovo kódování je použito jako součást Riceova algoritmu pro bezeztrátovou kompresi obrázků. Na grafu je vidět porovnání kompresních poměrů Riceova kódování a algoritmu Gzip.

Riceovo kódování může produkovat dlouhé posloupnosti jedniček pro podíl zakódovaný unárně, často je tedy nutné nastavit nějaký limit. Modifikovaná verze Rice-Golombova kódování umožňuje nahradit dlouhé sekvence jedniček pomocí rekurzivního Rice-Golombova kódování.

Reference

V tomto článku byl použit překlad textu z článku Golob coding na anglické Wikipedii.

Literatura

• Golomb, S.W. (1966). , Run-length encodings. IEEE Transactions on Information Theory, IT--12(3):399--401
• R. F. Rice (1971) and R. Plaunt, , "Adaptive Variable-Length Coding for Efficient Compression of Spacecraft Television Data, " IEEE Transactions on Communications, vol. 16(9), pp. 889–897, Dec. 1971.
• R. F. Rice (1979), "Some Practical Universal Noiseless Coding Techniques, " Jet Propulsion Laboratory, Pasadena, California, JPL Publication 79—22, Mar. 1979.
• Witten, Ian Moffat, Alistair Bell, Timothy. "Managing Gigabytes: Compressing and Indexing Documents and Images." Second Edition. Morgan Kaufmann Publishers, San Francisco CA. 1999 ISBN 1-55860-570-3
• David Salomon. "Data Compression",ISBN 0-387-95045-1.
• S. Büttcher, C. L. A. Clarke, and G. V. Cormack. Information Retrieval: Implementing and Evaluating Search Engines Archivováno 5. 10. 2020 na Wayback Machine.. MIT Press, Cambridge MA, 2010.

Externí odkazy

• Obrázky, zvuky či videa k tématu Golombovo kódování na Wikimedia Commons