Viterbiho algoritmus

Viterbiho algoritmus je algoritmus dynamického programování pro hledání/nalezení nejpravděpodobnější posloupnosti skrytých stavů – nazývané Viterbiho cesta – jehož výsledkem je posloupnost pozorovaných událostí, především v kontextu Markovových informačních zdrojů a skrytých Markovových modelů.

Pojmy „Viterbiho cesta“ a „Viterbiho algoritmus“ se používají i pro další podobné algoritmy dynamického programování, které hledají nejpravděpodobnější vysvětlení určitého pozorování. Například algoritmus dynamického programování pro statistické parsování lze použít na hledání nejpravděpodobnějšího bezkontextového odvození (parse) řetězce, který se někdy nazývá „Viterbiho odvození“.

Algoritmus navrhl Andrew Viterbi v roce 1967 pro dekódování konvolučních kódů na digitálních komunikačních linkách se šumem^[1]. Od té doby se používá při dekódování konvolučních kódů používaných v mobilních sítích CDMA a GSM i v běžných telefonních modemech, pro komunikaci se satelity a kosmickými sondami do vzdáleného vesmíru, i v bezdrátových sítích podle standardu 802.11. Často se používá i při rozpoznávání a syntéze řeči, v počítačové lingvistice, pro vyhledávání klíčových slov a v bioinformatice. Například při rozpoznávání řeči se zvukový signál považuje za pozorovanou posloupnost událostí, a textový řetězec za „skrytou příčinu“ zvukového signálu. Viterbiho algoritmus hledá nejpravděpodobnější řetězec textu k danému zvukovému signálu.

Algoritmus

Předpokládejme, že je dán skrytý Markovův model (HMM) se stavovým prostorem $S$, pravděpodobnostmi ${\mathrm{\pi <!--\; \pi \; -->}}_i$ začátku ve stavu $i$ (počáteční pravděpodobnosti), pravděpodobnostmi $a_{i,j}$ pro přechod ze stavu $i$ do stavu $j$ (přechodové pravděpodobnosti). Pokud pozorujeme výstupní posloupnost $y_1,\dots <!--\; \dots \; -->,y_T$, pak nejpravděpodobnější posloupnost stavů $x_1,\dots <!--\; \dots \; -->,x_T$, která produkuje pozorovaný výstup, je dána rekurentními vztahy:^[2]

kde $V_{t,k}$ je pravděpodobnost nejpravděpodobnější posloupnosti stavů odpovědné za prvních $t$ pozorování, jejíž koncový stav je $k$. Pro získání Viterbiho cesty lze používat zpětné ukazatele, které zachycují, jaký stav $x$ byl použit ve druhé rovnici. Nechť $Ptr(k,t)$ je funkce, která vrací hodnotu $x$ použitou pro výpočet $V_{t,k}$ pokud $t>1$, nebo $k$ pokud $t=1$. Pak:

(používáme standardní definici arg max).

Složitost tohoto algoritmu je $O(T\times <!--\; \times \; -->{\left|S\right|}^2)$.

Pseudokód

Pokud je dán prostor pozorování $O=\{o_1,o_2,\dots <!--\; \dots \; -->,o_N\}$, stavový prostor $S=\{s_1,s_2,\dots <!--\; \dots \; -->,s_K\}$, posloupnost pozorování $Y=\{y_1,y_2,\dots <!--\; \dots \; -->,y_T\}$, matice přechodů $A$ velikosti $K\times <!--\; \times \; -->K$ tak, že $A_{ij}$ obsahuje přechodovou pravděpodobnost přechodu ze stavu $s_i$ do stavu $s_j$, výstupní matice $B$ velikosti $K\times <!--\; \times \; -->N$ taková, že $B_{ij}$ obsahuje pravděpodobnosti pozorování $o_j$ ze stavu $s_i$, pole počátečních pravděpodobností $\mathrm{\pi <!--\; \pi \; -->}$ velikosti $K$ takové, že ${\mathrm{\pi <!--\; \pi \; -->}}_i$ obsahuje pravděpodobnost, že $x_1==s_i$. Nechť posloupnost $X=\{x_1,x_2,\dots <!--\; \dots \; -->,x_T\}$ je cestou, která generuje pozorování $Y=\{y_1,y_2,\dots <!--\; \dots \; -->,y_T\}$.

V tomto problému dynamického programování vytváříme dvě dvourozměrné tabulky $T_1,T_2$ velikosti $K\times <!--\; \times \; -->T$. Každý prvek $T_1$, $T_1[i,j]$, obsahuje pravděpodobnost zatím nejpravděpodobnější cesty $\stackrel{^<!--\; ^\; -->}{X}=\{{\stackrel{^<!--\; ^\; -->}{x}}_1,{\stackrel{^<!--\; ^\; -->}{x}}_2,\dots <!--\; \dots \; -->,{\stackrel{^<!--\; ^\; -->}{x}}_j\}$ s ${\stackrel{^<!--\; ^\; -->}{x}}_j=s_i$, která generuje $Y=\{y_1,y_2,\dots <!--\; \dots \; -->,y_j\}$. Každý prvek $T_2$, $T_2[i,j]$, obsahuje ${\stackrel{^<!--\; ^\; -->}{x}}_{j-<!--\; -\; -->1}$ zatím nejpravděpodobnější cesty $\stackrel{^<!--\; ^\; -->}{X}=\{{\stackrel{^<!--\; ^\; -->}{x}}_1,{\stackrel{^<!--\; ^\; -->}{x}}_2,\dots <!--\; \dots \; -->,{\stackrel{^<!--\; ^\; -->}{x}}_{j-<!--\; -\; -->1},{\stackrel{^<!--\; ^\; -->}{x}}_j\}$ pro každé $j,2\le <!--\; \le \; -->j\le <!--\; \le \; -->T$

Naplníme položky dvou tabulek $T_1[i,j],T_2[i,j]$ rostoucí posloupností $K\cdot <!--\; \cdot \; -->j+i$.

$T_1[i,j]=\underset{k}{max}\left(T_1\right[k,j-<!--\; -\; -->1]\cdot <!--\; \cdot \; -->A_{ki}\cdot <!--\; \cdot \; -->B_{i{y}_j})$, a

$T_2[i,j]=\arg <!--\; \; -->\underset{k}{max}\left(T_1\right[k,j-<!--\; -\; -->1]\cdot <!--\; \cdot \; -->A_{ki}\cdot <!--\; \cdot \; -->B_{i{y}_j})$

   VSTUP:  Prostor pozorování $O=\{o_1,o_2,\dots <!--\; \dots \; -->,o_N\}$, 
           stavový prostor $S=\{s_1,s_2,\dots <!--\; \dots \; -->,s_K\}$, 
           posloupnost pozorování  $Y=\{y_1,y_2,\dots <!--\; \dots \; -->,y_T\}$ taková, že $y_t==i$ pokud 
             pozorování v čase $t$ je $o_i$,
           matice přechodů $A$ velikosti $K\cdot <!--\; \cdot \; -->K$ tak, že $A_{ij}$ obsahuje přechodovou
             pravděpodobnost přechodu ze stavu $s_i$ do stavu $s_j$,
           emission matrix $B$ velikosti $K\cdot <!--\; \cdot \; -->N$ tak, že $B_{ij}$ obsahuje pravděpodobnost
             pozorování $o_j$ ze stavu $s_i$, 
           pole počátečních pravděpodobností $\mathrm{\pi <!--\; \pi \; -->}$ velikosti $K$ takové, že ${\mathrm{\pi <!--\; \pi \; -->}}_i$ obsahuje pravděpodobnost, že
             $x_1==s_i$
   VÝSTUP: Nejpravděpodobnější skrytá posloupnost stavů $X=\{x_1,x_2,\dots <!--\; \dots \; -->,x_T\}$
A01 function VITERBI(O, S, π, Y, A, B): X
A02     for each state si do
A03         T1[i,1]←πi$\cdot <!--\; \cdot \; -->$Bi$y_1$
A04         T2[i,1]←0
A05     end for
A06     for i←2,3,...,T do
A07         for each state sj do
A08             T1[j,i]←$\underset{k}{max}\left(T_1\right[k,i-<!--\; -\; -->1]\cdot <!--\; \cdot \; -->A_{kj}\cdot <!--\; \cdot \; -->B_{j{y}_i})$
A09             T2[j,i]←$\arg <!--\; \; -->\underset{k}{max}\left(T_1\right[k,i-<!--\; -\; -->1]\cdot <!--\; \cdot \; -->A_{kj}\cdot <!--\; \cdot \; -->B_{j{y}_i})$
A10         end for
A11     end for
A12     zT←$\arg <!--\; \; -->\underset{k}{max}\left(T_1\right[k,T\left]\right)$
A13     xT←szT
A14     for i←T,T-1,...,2 do
A15         zi-1←T2[zi,i]
A16         xi-1←szi-1
A17     end for
A18     return X
A19 end function

Příklad

Představte si lékaře, který má pečovat o ženu císaře trpící neustále se vracející nemocí. Projevy nemoci lze léčit; tato léčba je nepříjemná, ale nemocné uleví. Problém je, že lékař císařovnu nemůže sám vyšetřit, dostává pouze každý třetí den lísteček s informací, jak se císařovna cítí (výborně, slabě, na umření). Na základě těchto informací má lékař posoudit, zda je císařovna zdravá nebo nemocná a má být podrobena léčbě.

Lékař se domnívá, že zdravotní stav císařovny se chová jako diskrétní Markovův řetězec. Situaci, kdy lékař nemůže přímo zkoumat zdravotní stav císařovny, lze popsat jako skrytý Markovův model (HMM).

Lékař ví, jaká je pravděpodobnost nemoci císařovny a jak pravděpodobně se cítí, když je zdravá nebo nemocná. Jinak řečeno parametry HMM jsou známé. Mohou být reprezentovány následujícím programem v jazyce Python:

states = ('Zdravá', 'Nemocná')
 
observations = ('výborně', 'slabě', 'na umření')
 
start_probability = {'Zdravá': 0.6, 'Nemocná': 0.4}
 
transition_probability = {
   'Zdravá' : {'Zdravá': 0.7, 'Nemocná': 0.3},
   'Nemocná' : {'Zdravá': 0.4, 'Nemocná': 0.6},
   }
 
emission_probability = {
   'Zdravá' : {'výborně': 0.5, 'slabě': 0.4, 'na umření': 0.1},
   'Nemocná' : {'výborně': 0.1, 'slabě': 0.3, 'na umření': 0.6},
   }

V tomto kusu kódu start_probability reprezentuje lékařovo přesvědčení, v jakém stavu je HMM, když dostal první zprávu o tom, jak se císařovna cítí (jediné, co ví, je, že je častěji zdravá). Zde použité rozložení pravděpodobnosti není vyvážené; podle přechodové pravděpodobnosti by bylo přibližně {'Zdravá': 0.57, 'Nemocná': 0.43}. transition_probability reprezentuje změnu zdravotního stavu ve skrytém Markovově řetězci. V tomto příkladě je jenom 30% pravděpodobnost, že za tři dny bude císařovna nemocná, když je dnes zdravá. emission_probability reprezentuje pravděpodobnosti jednotlivých informací. Pokud je císařovna zdravá, je 50% pravděpodobnost, že se cítí výborně; pokud je nemocná, je 60% pravděpodobnost, že se cítí na umření.

Na obrázcích jsou použity názvy z původního anglického příkladu (skryté zdravotní stavy jsou Healthy = Zdravá, Fever = Nemocná; oznámené pocity jsou Dizzy = na umření, Cold = slabě, Normal = výborně)

Lékař dostal s postupně tři zprávy o tom, jak se císařovna cítí, první zpráva byla výborně, druhá slabě, třetí na umření a chce zjistit, jaká je nejpravděpodobnější posloupnost zdravotních stavů císařovny, která by vysvětlila tato pozorování? Odpověď poskytne Viterbiho algoritmus:

# Vizualizace Viterbiho algoritmu.
def print_dptable(V):
    print("    "),
    for i in range(len(V)): print("%7d" % i),
    print()

    for y in V[0].keys():
        print("%.5s: " % y),
        for t in range(len(V)):
            print("%.7s" % ("%f" % V[t][y])),
        print()

def viterbi(obs, states, start_p, trans_p, emit_p):
    V = [{}]
    path = {}

    # Initialize base cases (t == 0)
    for y in states:
        V[0][y] = start_p[y] * emit_p[y][obs[0]]
        path[y] = [y]

    # Run Viterbi for t > 0
    for t in range(1,len(obs)):
        V.append({})
        newpath = {}

        for y in states:
            (prob, state) = max([(V[t-1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
            V[t][y] = prob
            newpath[y] = path[state] + [y]

        # Don't need to remember the old paths
        path = newpath

    print_dptable(V)
    (prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
    return (prob, path[state])

Argumenty funkce viterbi jsou: obs je posloupnost pozorování, např. ['výborně', 'slabě', 'na umření']; states je množina skrytých stavů; start_p je start pravděpodobnost; trans_p jsou přechodové pravděpodobnosti; a emit_p jsou výstupní pravděpodobnosti. Pro jednoduchost kódu předpokládáme, že posloupnost pozorování obs je neprázdná a že trans_p[i][j] a emit_p[i][j] jsou definované pro všechny stavy i,j.

V našem příkladě se dopředný Viterbiho algoritmus používá takto:

def example():
    return viterbi(observations,
                   states,
                   start_probability,
                   transition_probability,
                   emission_probability)
print(example())

To ukazuje, že pozorování ['výborně', 'slabě', 'na umření'] byla s největší pravděpodobností generována posloupností stavů ['Zdravá', 'Zdravá', 'Nemocná']. Jinými slovy, na základě pozorovaných dat byla císařovna s největší pravděpodobností při odeslání první a druhé zprávy zdravá (poprvé se cítila výborně, podruhé slabě), a při odeslání třetí byla nemocná.

Funkci Viterbiho algoritmu lze vizualizovat pomocí trellis diagramu. Viterbiho cesta je v zásadě nejkratší cesta tímto trellisem. Trellis pro příklad s císařovnou je níže; odpovídající Viterbiho cesta je tučně:

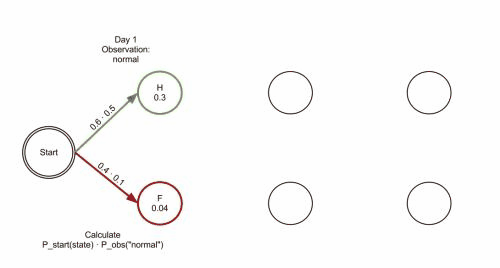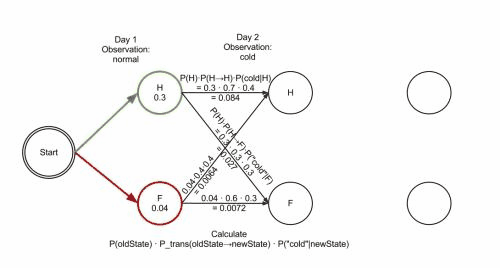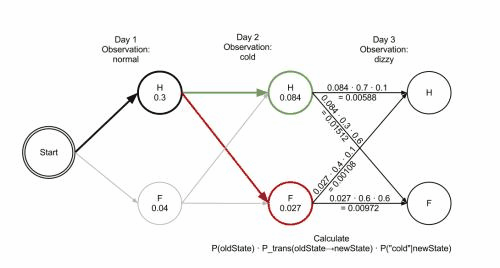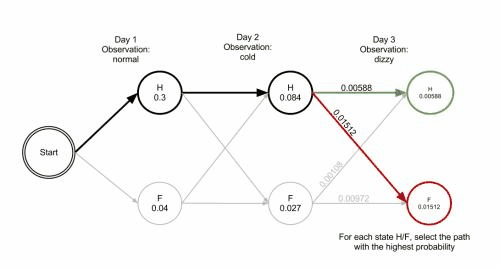
Při implementaci Viterbiho algoritmu je nutné zmínit, že mnoho jazyků používá aritmetiku s pohyblivou řádovou čárkou – pokud jsou hodnoty pravděpodobností malé, může dojít k podtečení výsledku. Obvyklá technika, jak se tomu vyhnout, je používat během celého výpočtu logaritmus pravděpodobnosti, tatáž technika použitá v Logarithmic Number System. Po skončení algoritmu lze získat správnou hodnotu pomocí exponenciální funkce.

Rozšíření

Zobecnění Viterbiho algoritmu nazývané max-sum algoritmus (nebo max-product algoritmus) lze použít pro nalezení nejpravděpodobnějšího přiřazení všech nebo určitých podmnožinách skrytých proměnných ve velkém množství grafických modelů, např. Bayesovské sítě, Markov náhodná pole a podmíněná náhodná pole. Skryté proměnné musí být obecně propojeny nějakým způsobem na HMM, s omezeným počtem spojení mezi proměnnými a určitým typem lineární struktury mezi proměnnými. Obecný algoritmus využívá mechanismus předávání zpráv a v zásadě se podobá algoritmu belief propagation (který je zobecněním forward-backward algoritmu).

Pomocí algoritmu nazývaného iterativní Viterbiho dekódování lze najít podposloupnost pozorování, která vyhovuje nejlépe (v průměru) dané HMM. Tento algoritmus navrhl Qi Wang, etc.^[3] pro zpracování turbo kódů. Iterativní Viterbi dekódování pracuje iterativně vyvoláním modifikovaného Viterbiho algoritmu, znovu odhadnutím skóre pro výplňku při konvergenci.

Nedávno byl navržen alternativní algoritmus, líný Viterbiho algoritmus^[4]. Pro mnoho kódů používaných v praxi, při rozumném šumu, je dekodér používající líný Viterbiho algoritmus mnohem rychlejší než tradiční Viterbiho dekodér^[5]. Líný Viterbiho algoritmus neexpanduje uzly, dokud to není opravdu nutné, a obvykle vyžaduje mnohem méně výpočtů, aby došel ke stejnému výsledku jako normální Viterbiho algoritmus – není ho však snadné hardwarově paralelizovat.

Existuje rozšíření Viterbiho algoritmu, aby pracoval s deterministickým konečným automatem pro zlepšení rychlosti při stochastické konverzi písmen na fonémy^[6].

Související články

• Baum–Welchův algoritmus
• Forward-backward algoritmus
• Forward algoritmus
• Samoopravný kód
• Viterbiho algoritmus s měkkým výstupem
• Viterbiho dekodér
• Markovův model i Skrytý Markovův model
• Part-of-speech tagging

Literatura

• Viterbi AJ. Error bounds for convolutional codes a an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory. 1967, s. 260–269. Dostupné online. DOI 10.1109/TIT.1967.1054010. Je zde použita šablona {{Cite journal}} označená jako k „pouze dočasnému použití“. (note: the Viterbi decoding algoritmus je described in section IV.) Subscription required.
• Feldman J, Abou-Faycal I, Frigo M. A Fast Maximum-Likelihood Decoder for Convolutional Codes. Vehicular Technology Conference. 2002, s. 371–375. DOI 10.1109/VETECF.2002.1040367. Je zde použita šablona {{Cite journal}} označená jako k „pouze dočasnému použití“.
• Forney GD. The Viterbi algorithm. Proceedings of the IEEE. 1973, s. 268–278. Dostupné online. DOI 10.1109/PROC.1973.9030. Je zde použita šablona {{Cite journal}} označená jako k „pouze dočasnému použití“. Subscription required.
• PRESS, WH; TEUKOLSKY, SA; VETTERLING, WT; FLANNERY, BP. Numerical Recipes: The Art of Scientific Computing. 3rd. vyd. [s.l.]: Cambridge University Press, 2007. ISBN 978-0-521-88068-8. Kapitola Section 16.2. Viterbi Decoding. Je zde použita šablona {{Cite book}} označená jako k „pouze dočasnému použití“.
• Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE. 1989, s. 257–286. DOI 10.1109/5.18626. Je zde použita šablona {{Cite journal}} označená jako k „pouze dočasnému použití“. (Describes the forward algoritmus and Viterbi algorithm for HMMs).
• Shinghal, R. a Godfried T. Toussaint, "Experiments in text recognition with the modified Viterbi algoritmus," IEEE Transactions on Pattern Analysis a Machine Intelligence, Vol. PAMI-l, April 1979, pp. 184–193.
• Shinghal, R. a Godfried T. Toussaint, "The sensitivity of the modified Viterbi algoritmus to the source statistics," IEEE Transactions on Pattern Analysis a Machine Intelligence, vol. PAMI-2, March 1980, pp. 181–185.

Reference

V tomto článku byl použit překlad textu z článku Viterbi algorithm na anglické Wikipedii.

Implementace

• C a Jazyk symbolických adres
• C
• C++
• C++ a Boost autor: Antonio Gulli
• C#
• F#
• Java
• Perl
• Prolog
• VHDL

Externí odkazy

• Obrázky, zvuky či videa k tématu Viterbiho algoritmus na Wikimedia Commons
• Implementace v jazyce Java, F#, Clojure, C# na Wikibooks
• Učební text^{[nedostupný zdroj]} o konvolučním kódování s Viterbiho dekódováním, autor: Chip Fleming
• Historie Viterbiho algoritmu, autor: David Forney
• Jemný úvod do dynamického programování a Viterbiho algoritmu
• Učební text o sadě nástrojů pro modelování skrytého Markovova modelu (implementovaná v jazyce C), který obsahuje popis Viterbiho algoritmu