Sinus

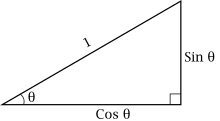
Sinus je goniometrická funkce nějakého úhlu. Zapisuje se jako sin θ, kde θ je velikost úhlu. Pro ostré úhly je definována v pravoúhlém trojúhelníku jako poměr protilehlé odvěsny a přepony (nejdelší strany). Definici lze konzistentně rozšířit jak na všechna reálná čísla, tak i do oboru komplexních čísel.

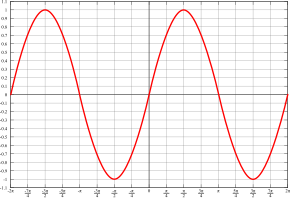
Grafem funkce sinus v reálném oboru je sinusoida.

Sinus na jednotkové kružnici

Sinus se jednoduše definuje na jednotkové kružnici (kružnici se středem v počátku a s poloměrem 1): Je-li α úhel, který svírá rameno s kladnou poloosou x (orientovaný od kladné poloosy x proti směru hodinových ručiček), je sin α roven y-ové souřadnici průsečíku této kružnice s koncovým ramenem úhlu α, jinak řečeno, rovná se délce kolmice spuštěné z tohoto bodu na osu x. Délce úsečky z počátku k patě této kolmice, přesněji (s ohledem na znaménko) x-ové souřadnici průsečíku jednotkové kružnice s koncovým ramenem úhlu α, je pak roven cos α. Poloměr, kolmice a tato úsečka tvoří pravoúhlý trojúhelník, pro nějž platí Pythagorova věta, takže také platí:

$(\sin <!--\; \; -->\mathrm{\alpha <!--\; \alpha \; -->}{)}^2+(\cos <!--\; \; -->\mathrm{\alpha <!--\; \alpha \; -->}{)}^2=1$.

Na jednotkové kružnici je také vidět, že sinus je v prvním a druhém kvadrantu nezáporný (≥ 0), kdežto ve třetím a čtvrtém nekladný (≤ 0). V prvním a čtvrtém kvadrantu je rostoucí, ve druhém a třetím klesající.

Protože zřejmě platí, že

$\sin <!--\; \; -->\mathrm{\alpha <!--\; \alpha \; -->}=\sin <!--\; \; -->(\mathrm{\alpha <!--\; \alpha \; -->}+k\cdot <!--\; \cdot \; -->2\mathrm{\pi <!--\; \pi \; -->})$ (resp. $\sin <!--\; \; -->(\mathrm{\alpha <!--\; \alpha \; -->}+k\cdot <!--\; \cdot \; -->{360}^{\circ <!--\; \circ \; -->}$)),

kde $k$ je libovolné celé číslo, lze funkci sinus rozšířit i na záporné úhly a konzistentně definovat jako funkci na celé množině reálných čísel. Sinusoida pak zhruba (při nekonečně dlouhé ojnici) popisuje například pohyb pístu ve válci spalovacího motoru.

Sinus v reálném oboru

Reálná funkce reálné proměnné $y=\sin <!--\; \; -->x$ má následující vlastnosti (kde $k$ je libovolné celé číslo):

• Definiční obor: $R$ (reálná čísla)
• Obor hodnot: $⟨<!--\; ⟨\; -->-<!--\; -\; -->1;1⟩<!--\; ⟩\; -->$
• Rostoucí: v každém intervalu $\left(-<!--\; -\; -->\frac{1}{2}\mathrm{\pi <!--\; \pi \; -->}+2k\mathrm{\pi <!--\; \pi \; -->};\frac{1}{2}\mathrm{\pi <!--\; \pi \; -->}+2k\mathrm{\pi <!--\; \pi \; -->}\right)$
• Klesající: v každém intervalu $\left(\frac{1}{2}\mathrm{\pi <!--\; \pi \; -->}+2k\mathrm{\pi <!--\; \pi \; -->};\frac{3}{2}\mathrm{\pi <!--\; \pi \; -->}+2k\mathrm{\pi <!--\; \pi \; -->}\right)$
• Maximum je $1$ (v bodech $x=\frac{1}{2}\mathrm{\pi <!--\; \pi \; -->}+2k\mathrm{\pi <!--\; \pi \; -->}$)
• Minimum je $-<!--\; -\; -->1$ (v bodech $x=-<!--\; -\; -->\frac{1}{2}\mathrm{\pi <!--\; \pi \; -->}+2k\mathrm{\pi <!--\; \pi \; -->}$)
• Derivace: $(\sin <!--\; \; -->x{)}^{\prime }=\cos <!--\; \; -->x$
• Primitivní funkce: $\int <!--\; \int \; -->\sin <!--\; \; -->xdx=-<!--\; -\; -->\cos <!--\; \; -->x+C;C\in <!--\; \in \; -->R$
• Taylorova řada: $\sin <!--\; \; -->x=x-<!--\; -\; -->\frac{x^3}{3!}+\frac{x^5}{5!}-<!--\; -\; -->\frac{x^7}{7!}+\dots <!--\; \dots \; -->=\underset{n=0}{\overset{\mathrm{\infty <!--\; \infty \; -->}}{\sum <!--\; \sum \; -->}}\frac{(-<!--\; -\; -->1{)}^n{x}^{2n+1}}{(2n+1)!}$
• Inverzní funkce (na intervalu $⟨<!--\; ⟨\; -->-<!--\; -\; -->1;1⟩<!--\; ⟩\; -->$ a oborem hodnot $⟨<!--\; ⟨\; -->-<!--\; -\; -->\frac{1}{2}\mathrm{\pi <!--\; \pi \; -->};\frac{1}{2}\mathrm{\pi <!--\; \pi \; -->}⟩<!--\; ⟩\; -->$): arkus sinus (arcsin)
• Sinus doplňkového úhlu: $\sin <!--\; \; -->(\frac{\mathrm{\pi <!--\; \pi \; -->}}{2}-<!--\; -\; -->x)=\cos <!--\; \; -->x$
• Sinus dvojnásobného argumentu: $\sin <!--\; \; -->2x=2\sin <!--\; \; -->x\cos <!--\; \; -->x$
• Sinus polovičního argumentu: ${\sin }^2<!--\; \; -->x/2=\frac{1-<!--\; -\; -->\cos <!--\; \; -->x}{2}$
• délka sinusoidy (na intervalu periody): Navinutím grafu funkce $y=A\sin <!--\; \; -->\left(x/r\right)$ na válec o poloměru $r$ vznikne elipsa o poloosách $r$, $\sqrt{r^2+A^2}$. Díky této transformaci lze k výpočtu použít četné nástroje pro obvod elipsy.
• funkce sinus:
  • je lichá
  • je omezená shora i zdola
  • je periodická s nejmenší periodou $2\mathrm{\pi <!--\; \pi \; -->}$
  • není prostá

Sinus a kvadranty

Pohybujeme se v kartézské soustavě souřadnic se čtyřmi kvadranty. Níže uvedená tabulka zobrazuje několik klíčových vlastností sinusové funkce dle konkrétního kvadrantu. Pro argumenty mimo tabulku lze vypočítat odpovídající informace pomocí periodicity funkce sinus.

Následující tabulka uvádí základní hodnoty na hranicích kvadrantů:

Hodnoty sinus na jednotkové kružnici

Tabulka pro orientaci v jednotkové kružnici ve stupních a radiánech:

Tabulka hodnot po 90° v jednotkové kružnici:

Výpočty hodnot

Sinus, stejně jako ostatní goniometrické funkce, patří mezi tzv. transcendentální funkce, jejichž hodnoty nelze přímo vypočítat pomocí elementárních operací. Pro výpočty s goniometrickými funkcemi se používají počítače a vědecké kalkulátory, takže jejich hodnoty většinou není třeba počítat. Pro ruční výpočet se používaly tabulky, kde byly tyto hodnoty už vypočteny pro určité hodnoty úhlů, a pro mezilehlé hodnoty se používala interpolace. Pro výpočty například při tvorbě takových tabulek se používají nekonečné řady. V počítačích a kalkulátorech se hodnoty goniometrických funkcí obvykle aproximují pomocí snáze vypočítatelných hodnot obvykle Čebyševových polynomů nebo nekonečných řad (Taylorova řada)

Hodnoty goniometrických funkcí lze však přesně určit pro všechny násobky 60° a 45°, a to následujícím způsobem:

Mějme rovnoramenný pravoúhlý trojúhelník s délkami odvěsen a=b=1; úhly při přeponě jsou stejné a tedy rovné $\mathrm{\pi <!--\; \pi \; -->}/4$ (45°). Pak podle Pythagorovy věty:

$c=\sqrt{a^2+b^2}=\sqrt{2}$

a tedy ovšem

$\sin <!--\; \; -->\frac{\mathrm{\pi <!--\; \pi \; -->}}{4}=\cos <!--\; \; -->\frac{\mathrm{\pi <!--\; \pi \; -->}}{4}=\frac{\sqrt{2}}{2}$

$\text{tg}\frac{\mathrm{\pi <!--\; \pi \; -->}}{4}=\frac{\sqrt{2}}{\sqrt{2}}=1$

Goniometrické funkce úhlů $\mathrm{\pi <!--\; \pi \; -->}/3$ radiánů (60°) a $\mathrm{\pi <!--\; \pi \; -->}/6$ radiánů (30°) se určí pomocí rovnostranného trojúhelníka se stranami délky 1. Všechny jeho úhly jsou rovny $\mathrm{\pi <!--\; \pi \; -->}/3$ radiánů (60°). Když ho rozdělíme na poloviny, získáme pravoúhlý trojúhelník s úhly o velikostech $\mathrm{\pi <!--\; \pi \; -->}/6$ a $\mathrm{\pi <!--\; \pi \; -->}/3$. Jeho kratší odvěsna má délku $1/2$, delší $\sqrt{3}/2$ a přepona délku 1. Pak tedy:

$\sin <!--\; \; -->\frac{\mathrm{\pi <!--\; \pi \; -->}}{6}=\cos <!--\; \; -->\frac{\mathrm{\pi <!--\; \pi \; -->}}{3}=\frac{1}{2}$

$\cos <!--\; \; -->\frac{\mathrm{\pi <!--\; \pi \; -->}}{6}=\sin <!--\; \; -->\frac{\mathrm{\pi <!--\; \pi \; -->}}{3}=\frac{\sqrt{3}}{2}$

$\text{tg}\frac{\mathrm{\pi <!--\; \pi \; -->}}{6}=\text{cotg}\frac{\mathrm{\pi <!--\; \pi \; -->}}{3}=\frac{1}{\sqrt{3}}$

Sinus v komplexním oboru

Funkce sinus je v komplexních číslech definována součtem řady

$\sin <!--\; \; -->z=z-<!--\; -\; -->\frac{z^3}{3!}+\frac{z^5}{5!}-<!--\; -\; -->\frac{z^7}{7!}+\dots <!--\; \dots \; -->=\underset{n=0}{\overset{\mathrm{\infty <!--\; \infty \; -->}}{\sum <!--\; \sum \; -->}}\frac{(-<!--\; -\; -->1{)}^n{z}^{2n+1}}{(2n+1)!},$

která konverguje na celé komplexní rovině. Pro každá komplexní čísla $z$, $z_1$ a $z_2$ platí:

$\sin <!--\; \; -->z=\frac{e^{iz}-<!--\; -\; -->e^{-<!--\; -\; -->iz}}{2i},$

$\sin <!--\; \; -->\left(z_1+z_2\right)=\sin <!--\; \; -->z_1\cos <!--\; \; -->z_2+\cos <!--\; \; -->z_1\sin <!--\; \; -->z_2,$

$\sin <!--\; \; -->iz=i\sinh <!--\; \; -->z.$

Tyto vzorce plynou přímo z příslušných definičních mocninných řad daných funkcí. Sinus je na celé komplexní rovině jednoznačná holomorfní funkce.

Odkazy

Související články

• Sinová věta
• Kosinus

Externí odkazy

• Obrázky, zvuky či videa k tématu sinus na Wikimedia Commons
• Slovníkové heslo sinus ve Wikislovníku
• Sinus v encyklopedii MathWorld (anglicky)
• Vzorce obsahující sinus na functions.wolfram.com (anglicky)